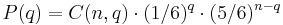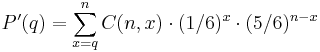Liar's dice
Liar's dice, or Liar dice, with roots originating in South America and popularized in early Spanish History, was brought to Spain by the Spanish conqueror Francisco Pizarro during the 16th century. It became extremely popular in Hong Kong and consequentially China. As it is listed under the 10 most popular games in China, where most bars and clubs will have dice and cups stationed at tables. [1] Liar's Dice is known for being a game in pirate history, and a name for a class of dice games for two or more players. They are easy to learn, require little equipment, and can be played as gambling or drinking games. Playing them well requires the ability to deceive and detect an opponent's deception. When a player loses a hand, then the losing player starts the next round.
Versions of the game are known as Deception Dice (U.S.A. manufactured), Diception, Dudo or Cachito in South America. The equivalent drinking game is sometimes called Mexicali or Mexican in the United States; the latter term may be a corruption of Mäxchen ("Little Max"), the name by which a similar game, called Mia, is known in Germany, while Liar's dice is known in Germany as Bluff.
There are at least three different versions of Liar's Dice; it's uncertain which version is the original. In all of them, dice are rolled in a concealed fashion and bids made about the result of the roll. Players must then either raise the bid or challenge the previous bid in turn. For the purposes of this article, the three versions discussed are referred to as "individual hand", "common hand", and "Mexican".
In "common hand", each player has a set of dice, all players roll one and the bids relate to the dice each player can see (their hand) plus all the concealed dice (the other players' hands).
In "individual hand", there is one set of dice which is passed from player to player. The bids relate to the dice as they are in front of the bidder after selected dice have been re-rolled.
Contents |
Rules (common hand)
This is the version that is used in the movie Pirates of the Caribbean: Dead Man's Chest and the video game Red Dead Redemption.
Five six-sided dice with traditional dot faces are generally used per player, with dice cups used for concealment. Poker dice can also be used, but some systems for bidding become difficult or impossible to use.
Each round, the players roll their dice while keeping them concealed from the other players. One player begins bidding, picking a quantity of a face 2 through 6. The quantity states the player's opinion on how many of the chosen face have been rolled in total on the table. A 1 ("ace") is often wild and counts as the stated face of the current bid, however the game can also be played without wilds (see variants). In a five-dice, three-player game with wilds, the lowest bid is "one 2" and the highest bid "five 6s".
Each player has two choices during his turn: make a higher bid, or challenge the previous bid as being wrong. Raising the bid means either increasing the quantity, or the face value, or both, according to the specific bidding rules used. Different bidding rule sets are described below.
If the current player thinks the previous player's bid is wrong, he challenges it, and then all dice are revealed to determine whether the bid was valid. If the number of the relevant face revealed is at least as high as the bid, then the bid is valid, in which case the bidder wins. Otherwise, the challenger wins. A challenge is generally indicated by simply revealing one's dice, though it is customary to verbally make the challenge, by saying "I call you up", "I call", "You're a liar", or simply "Liar".
- Example: if a bid of "seven fours" is challenged, the bid is successful (and the player who made it wins) if there are seven or more fours (including aces if they are wild). The bid fails (the bidder is a Liar and the challenger wins) if there are fewer than seven fours (including aces if they are wild).
Bidding rules
The most common systems for bidding are listed below, in order of the amount of restriction they place on bidders. All variants are described in relation to the face value and quantity of the previous bid.
- The player may bid an increased quantity of the same face, or any quantity of a higher face. Given a bid of "three twos", the minimum raise is either "four twos" or any quantity of "threes". This is very common as it generally gives players many options, allowing for the most information to be gained. Using this ruleset, face value of the bid cannot be lowered except with a popular rule variant; the next ruleset, however, is similar and allows for reduction in face.
- The player may bid an increased quantity of any face, or the same quantity of a higher face. Given a bid of "four fours", the minimum raise is five of any face, or "four fives". This is the most common ruleset in packaged games as it is very similar to Poker's emphasis on quantity over rank in hand rankings (three twos is better than a pair of kings). It also allows a player to re-assert a lower face value believed to be predominant.
- The player may bid any quantity of any face, as long as either the quantity or face is higher than the higher of the two numbers of the previous bid. Given a bid of "five threes", the minimum bid must have a six, either six of any face or any quantity of "sixes". The bid can go higher than six; the number raised is then always the quantity. Either this system or the previous one was used in the game featured in Pirates of the Caribbean: Dead Man's Chest; the bidding in that game conforms to both systems. They are however different; a bid of "five fours" following "four fives" is legal in the preceding system while illegal in this one.
- The player may bid any quantity of any face, as long as the product of the quantity and face is higher than that of the previous bid. A bid of "three threes" multiplies to nine, so the minimum raise is "two fives" or "five twos", the product of either being ten. This system is uncommon, especially as a drinking game due to the arithmetic required, but is simple for a computer to check and is sometimes used to add an educational element. Because "aces" as their face value become largely worthless very quickly, this system is predominantly used with wild aces.
- The player may bid a higher quantity of the same face, or the same quantity of a higher face. Given a bid of "six fives", the minimum bid is either "six sixes" or "seven fives". This is common in computer versions of the game as the rules can be enforced "real-time" by simply preventing a lowering of face or quantity. Because of this same simplicity, it is also common in smaller games, but as the most restrictive of these systems, rounds tend to be very short as the bid quickly becomes improbable.
Raises must be at least the minimum, however the current player may raise the bid to any legal bid. Given "four fours", a player may (in any of these systems) call "seven sixes". Such "bid jumping" has strategic value, but a large increase such as in this example has a high probability of being incorrect, and so is likely to trigger a challenge. It is also considered bad form in some groups, as bid jumping reduces the amount of information that can normally be gained by more conservative raises, and makes for shorter games.
Variants
- The game can be played without wild aces. This simplifies game play and odds calculation, and is a good way to introduce beginners to the game. Ones then become similar to any other value. This variant is often used with a less restrictive bidding system, particularly one that allows a reduction in the face value of the bid.
- To commence play, the dice are often rolled on cue. Participants chant "Uchi Uchi Uchi MA!" with emphasis on the MA. The dice hit the playing surface hidden from view as players say MA.
- A player that loses a challenge loses a die, and the next round begins. If there are three players and on the first round, Player 1 loses a die, then in the second round Player 1 has only four dice, whereas Players 2 and 3 still have five. This puts Player 1 at a disadvantage as he has less information than the other players about the dice. A player with no dice is out of the game.
- Another variation that can be played is for the loser of a challenge to give one die to the winner of that challenge. If Player 2 challenged Player 1's bid in the previous example, and Player 2 won, then at the beginning of the next round Player 1 would have four dice and Player 2 would have six dice.
- Also, the amount of dice lost can be decided to be the difference in bid and actual outcome, e.g. a player bids five 4s when another calls the bluff, but there altogether are only two 4s and one 1; hence, the loss will be two dice. This leads to a sounder relationship between the probability and cost of over-bidding.
- In variants where dice are lost over the course of the game it is customary to start with more dice; typically as many as there are available.
- In a drinking variant called snyd used in Denmark, everybody but the loser of the challenge discard a die. The last person to have dice is the loser and buys the table a round.
- Instead of the current player being the only one who can challenge (or "call up") the previously-made bid, any player may challenge a bid at any time. This is challenging out-of-sequence. In the case of multiple out-of-sequence challenges at the same time, the person closest to the bidder in the normal direction of play is the challenger. Alternatively, multiple challengers could be honored, with rules on how winnings or losses are paid out among challengers set out beforehand. This variant is uncommon, but adds a heightened tension to bidding as a challenge may come from anywhere. Penalties for making an out-of-sequence challenge are often included with this variant, such as the challenger being required to double their wager or losing double the dice from their hand if they are incorrect.
- When a bidding system is used that does not allow the reduction of face value when raising a bid (such as the first or fifth listed system above), a player may elect to choose one or more dice of matching value from under his cup, place them outside the cup in view of the other players, re-roll the remaining dice, and make a bid on the shown face value higher than the quantity shown. This may be done only once per round (sometimes once per player per round), and the player doing this must have at least one die left under his cup after taking out the dice to show others. This is regarded as an emergency option when a player believes that the previous bid is correct but is unwilling to raise. It allows the player to escape the situation and also changes the dice in play, with the disadvantage of giving up some information about the player's dice.
- 1s are only wild for the player who rolled them. (So to make a bid, you count natural rolls from all players, and ones from your own roll.)
- 1s are bid in a special manner. 1s are wild when the bid is on any face value other than 1. When switching the bid to 1s (if allowed by the bidding rules), the quantity must be a minimum of half (rounded up) the previous bid's quantity. To switch back to a non-1 face, the quantity must either be double the number of 1s bid or one greater than the last non-1 bid, whichever is greater. For example, a bid of "four 5s" could be followed by a bid of "two 1s", which could in turn be followed by "three 1s" or five of any face. If "three 1s" is bid and the next bidder wishes to change the face value of his bid, a quantity of six or more of the new face must be bid. The idea is that when 1s are bid when they are normally wild, there is no longer a wild value that can help the player make that bid. Therefore the odds, in general, of any quantity of 1s having been rolled are roughly equal to double that quantity of both wild aces and any other value combined.
- 1s are only wild if not called on the first bid. This is an extremely common variant on the US West Coast and in Bangkok, Thailand. When 1s are not wild, all face values called are said to be "natural". This makes one 1 a very common call, especially by a player with few dice left, and can significantly change the strategy of the game since removing the possibility of wilds halves the expected number of any face value.
- 6 is wild instead of 1. This is uncommon, as most packaged versions of the game use dice with a special shape (often a star) in place of the dot on the "1" face to denote wilds.
- When a player has no two dice with the same face, he may choose to pass once in a game round. If he does so, the bid won't be raised. The next player can raise the bid using standard rules, or call the bluff. By doing so, he challenges the claim of the passing player having no two dice with the same face. If there are consecutive pass bids, the player currently taking his turn may challenge any of the previous distinctness claims. This is commonly used in multi-round games where dice are removed from the game, as it helps players with few dice left to gain more information about the other dice without risking being called a liar.
- Instead of raising or challenging, the player can bet that the current bid is exactly correct (usually announced by calling "Spot On"). Such a call, like "Liar", ends the round. If the number is higher or lower, the player loses to the previous bidder, however if they are correct, they win. This allows a player who believes the previous bidder has made the best correct bid to attempt to "steal" the win. "Spot-on" calls have a far higher probability of being wrong, and so the reward for a correct "Spot-on" call is generally higher; a "spot-on" call may be used to gain a previously lost die for instance, or to make all other players pay the agreed penalty for losing (giving up a die, drinking, paying out) instead of just the previous bidder.
- Such an increased penalty may also be applied after a bid is challenged normally and turns out to be exactly correct.
- Stairs. In the Danish variant 'snyd' a complete set of dices starting with 1 and ascending, such as 1, 2 and 3 with three dices counts as a stair, and are then all treated as 1's, in this case giving three wildcards. This introduces more wildcards in the later part of the game when there are fewer dice.
- Diception. In this version of the game, there is a Second Chance Cube. The Second Chance Cube is larger than the rest of the dice and contains unique instructions printed on various facets of the dice. The loser of each round has the opportunity to roll the Second Chance Cube and in most cases it is a wise decision. The Second Chance Cube will instruct the entire table on next steps. For example 50% of the time the outcome remains the same with the loser still needing to forfeit a die. But, there is also a 50% chance that the outcome will be completely different. For example the person that just won may have to forfeit a die, or the rest of the table may have to surrender dice. The Second Chance Cube has the ability to drastically alter the outcome of the game!
Gambling
There are a number of different ways to gamble with Liar's Dice. The simplest and probably most popular scheme is for all players to agree on a wager for the game before the first round, and for the game to be played winner-take-all using the multi-round "lose a round, lose a die" variant. Another popular method is played round-by-round with no dice lost, and the loser pays the winner their wager after each round, with other players breaking even.
Drinking game
Also known as Mexacali,[2] a popular way of playing Liar's Dice as a drinking game is to play in rounds, and the losing player or players for each round take a drink of alcohol. If played with the variants where players lose dice when they lose a round, they may be required to take a drink for each die lost and an additional pre-arranged number of drinks upon being eliminated from the game, or a drink for every round played thereafter until the game is over. Care must be taken with this last variant; the player eliminated first from a game with 4 or 5 players may have to drink 15 or 20 drinks in a relatively short time if this rule is in effect using shots or full beers as "drinks". Sometimes the drinking is based upon the difference between the quantities bid and revealed. For a failed out-of-sequence challenge, the out-of-sequence challenger drinks a greater quantity (e.g. double). If played with "Spot On" calls, a successful "Spot On" call means everyone else drinks, while a failed call means the caller drinks double.
Elements of common hand strategy
Playing Liar's dice involves many subtleties and interpersonal skills similar to other bluffing games such as Poker. However, there are some universal elements of strategy.
Perhaps foremost, a bid gives others at the table information. Players, through subsequent bids, reveal the players' confidence in the quantity of each face value rolled. A player with two or three of a certain face value under his or her own cup may make a bid favoring that face value. Players can thus use these bids to build a mental picture of the unknown values, which either strengthens or weakens their confidence in a bid they are considering. Others may consider a bid as evidence it is true, and if their own dice support the same conclusion, may increase the bid on that face value, or if their dice refute it may bid on a different face, or challenge the previous bid.
Conversely, bids can also be bluffs. Bluffs in Liar's Dice can be split into two main categories; early bluffs and late bluffs. An early bluff, for instance "three threes" when the player making the bid has no threes under his cup, is likely to be correct by simple probability (depending on the number of players), however, other players may believe the bidder made that bid because his or her dice supported it. Thus, the bluff is false information that can lead to incorrect bids being made on that face value. Players will thus attempt to trick other players into overbidding by use of early bluffs to inflate a particular face value. A late bluff, on the other hand, is usually less voluntary; the player is often unwilling to challenge a bid, but as a higher bid is even more likely to be incorrect it is even less appealing. A late bluff is thus a critical part of the game; convincing bluffs, as well as reliable detection of bluffs, allow the player to avoid being challenged on an incorrect bid.
As with any game of chance, probability is highly important. The key element is the "expected quantity"; the quantity of any face value that has the highest probability of being present. For six-sided dice, the expected quantity is one-sixth the number of dice in play, rounded down. When wilds are used, the expected quantity is doubled as players can expect as many aces, on average, as any other value. Because each rolled die is independent of all others, any combination of values is possible, however the "expected quantity" has a greater than 50% chance of being correct, and the highest probability of being exactly correct ("Spot On"). For example, when 15 dice are in play and wilds are used, the expected quantity is 5. The chances of a bid of 5 being correct are about 59.5%; in contrast, the chances of a bid of 8 being correct are only about 8.8%.
However, a high bid is not necessarily incorrect, because bids incorporate information the player knows. A player who holds a preponderance of a single value (for instance, four out of the five dice in his hand are threes) may make a bid, with fifteen dice on the table, of "six threes". To an outside observer who sees none of the dice, this has an extremely low probability of being correct (even with wilds), however since the player knows the value of five of those dice, the player is actually betting that there are two additional threes among the ten unknown dice. This is far more likely to be true.
Basic dice odds
For a given number of unknown dice n, the probability that exactly a certain quantity q of any face value are showing, P(q), is
Where C(n,q) is the number of unique subsets of q dice out of the set of n unknown dice. In other words, the number of dice with any particular face value follows the binomial distribution 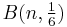 .
.
For the same n, the probability P'(q) that at least q dice are showing a given face is the sum of P(x) for all x such that q ≤ x ≤ n, or
These equations, entered into a spreadsheet program, can be used to calculate and chart the probability of exactly q and at least q for any or multiple n. For most purposes, it is sufficient to know the following facts of dice probability:
- The expected quantity of any face value among a number of unknown dice is one-sixth the total unknown dice.
- A bid of the expected quantity (or twice the expected value when playing with wilds), rounded down, has a greater than 50% chance of being correct and the highest chance of being exactly correct.
Rules (individual hand)
Players: 2
Equipment: two dice cups, 10 dice (can be regular dice or poker dice), a removable screen (optional).
Setup: Each player gets one dice cup, 5 dice, and a removable screen in between. The removable screen is not required, and in which case, the player can just use the cup to block the view of the other player. Nobody should be able to see anybody's dice unless a bluff is called.
The Play: The game starts with each player rolling one die each to determine who will be the first caller. The player with the highest number wins, and in the event of a tie, roll again.
Both players roll their five dice at the same time, then examine their hands. The player that won the first roll gets to call his hand first. All hands are called in style similar to poker, and is as follows, from highest to lowest;
Five of a Kind: ex. 44444
Four of a Kind: ex. 22225
Full House: ex. 66111
High Straight: 23456
Low Straight: 12345
Three of a Kind: ex. 44432
Two Pair: 22551
Pair: 66532
Runt: 13456
Hands have to be called in full. Instead of merely announcing "Full House", one must say "Full House, ones over sixes". Numbers not related to the call do not need to be noted.
After the Caller has announced his hand, the second player has three options: 1) Call their own hand, 2) re-roll some or all of their dice or 3) call the bluff.
In the first instance, the call must be higher than the previous call.
In the second instance, the player can re-roll some or all of their dice to try to obtain a better hand. The player has three tries to roll a better hand. After the first re-roll, the second player may re-call his hand, but only if they can re-call it higher than the Callers hand. If the Second player re-calls, the onus returns to the Caller to Call their own hand, Re-roll or call the bluff. Once a player has performed their first re-roll, they lose their ability to call the bluff until their next turn. If the player exhausts all three re-rolls, then the bluff is automatically called, in which both players must remove the screen/their cups from the table and reveal their dice.
In the third instance, the round immediately comes to an end, with the accused bluffer revealing their dice. If the Caller was bluffing, and didn't have as high as a hand as he called, the Caller loses and the Second player wins. However, if the Caller was not bluffing, and has the hand that he called, or a better hand than he called, the Caller wins and the Second player loses, regardless of the hand the player calling the bluff has.[3]
Stanford variation of individual hand
The Stanford variation is played with one set of six standard dice. Play is still the same, although the points are often eliminated. Players can reveal dice or remove them from view, as well as roll them inside or outside of the box.
Bids
Hands are evaluated in this manner
- More of a kind is always better than less of a kind
- Higher numbers beat lower numbers
- If there is a tie in the major part of the hand, evaluate the next part of the hand.
Here are some examples
- 111123 is better than 666555, because four 1s are better than three 6s and three 5s.
- 666432 is better than 555444, because three 6s are better than three 5s.
- 555443 is better than 555621, because although both hands have three 5s, the first has two 4s while the second has a 6 high
When making the claim, the bidder does not describe every die in the hand. Instead, the hand is assumed to be the minimum hand to fit the claim. For example, the call "Three 6s" is shorthand for the minimum hand that has three 6s, 666321. The call "Four of a kind and a pair" is shorthand for 111122, the minimum hand to fit the description.
The term "Minimum Raise" means "the next greatest hand."
You may roll die inside the box or outside the box. You cannot lie about how many die you roll, though you can conceal which die you are rolling.
Rules (Mexican)
This variation is common in Central Wisconsin, but may be played in a similar fashion throughout the Midwest. The emphasis is not so much on what is rolled as in player skill and guile. This is a drinking game, in that the loser of any phase of the competition must take a drink of an alcoholic beverage. Most bars in the Midwest have dice cups; simply ask and you can play too!
The game is best played in a tavern among three to six players (two to eight is acceptable) sitting at the bar. It adds to the camaraderie to be seated at a corner or, if the topography of the bar permits, in a semicircle or U-shaped outcrop.
The game starts by one person rolling two dice (some variations play with three dice) under a cup "to open." Rolling under a cup keeps the result of the roll hidden from the next player. The roller then peeks under the cup to see what was rolled.
In every case except doubles (both dice are the same) and a few special rolls, the roll is scored by placing the higher die result in the 10s place and the lower result in the 1s place. Therefore,
In order from worst to best (along with common nicknames and variants of same), the rolls are: 4-1 (In some variations, 41 allows the roller to impose a drink upon another player—treat as Social or Reverse afterward (see below)) 4-2 4-3 5-1 5-2 5-3 5-4 (Betty Ford) 6-1 6-2 6-3 6-4 6-5 1-1 (Snake Eyes) 2-2 (Ducks) 3-3 (Coke Lines) 4-4 (Windows) 5-5 (Snowflakes, Tees in a Wee) 6-6 (Boxcars, Box Car Willie, Bee Cee Dubs) 2-1 (Mexican, Benito Juarez etc.)
A roll (or claim) of "Mexican" obligates the losing player to consume the rest of the beverage in one's glass.
Special rolls: 3-1 Social (Everyone drinks, cancel all previous rolls, roll again to open); 3-2 Reverse (Change direction, cancel all previous rolls, roll again to open)
In consideration of the above scoring, the roller evaluates the roll and then relates to the next player the value of the roll—HOWEVER—the roller is under no obligation to be truthful about the roll.
The next player may do one of two things:
- If he believes the roller, he simply takes the dice (without looking at the result), and tries to roll to the next player something equal to or higher than what the previous roller claimed. If he does not roll something equal to or higher, he must attempt to bluff the following player by declaring a higher (or tie) score. Alternatively, he may sheepishly admit a loss, drink, and pass the dice.
- If he does not believe the roller, the cup is lifted, revealing the roller's hand.
- If the roller was bluffing, the roller must drink. The winning player starts over with no previous roll value to beat (rolls "to open" or "fresh").
- If the roller was telling the truth, the challenger must drink, and the winning player rolls again "to open" to the losing player.
Play always starts "fresh" or "to open" after someone drinks.
Special Considerations
Sloppy Dice:
Every die dropped on the floor equals one drink for the last person to touch the die or dice in question. It's possible for a non-rolling player to owe a drink if he tries to catch the rolling player's dice and fails. A cup on the floor incurs no penalty.
If one die sloppily ends up not being under the cup after a roller's roll, the roller may leave the exposed die and claim a score based on the exposed die and the die under the cup. Belief and disbelief proceeds normally.
Customs and Courtesies:
1. Typically, "Betty Ford" is believed, even to tie. This is based on the sense that if one can't beat a 5-4, one ought to find a different game. Nevertheless, a properly disbelieved Betty Ford has its place.
2. On a Social or Reverse roll, the obligation is upon the roller to prove it, not on the next player to believe or disbelieve it. A claim of "show it" is always appropriate on a Social or Reverse call.
3. Unless cheating is directly detrimental to a player, a player won't typically expose a cheating player to the player being cheated.
4. A player caught in the act of cheating will admit it. In other words, you tried, but got caught. Cowboy up and admit it.
5. Cheating
Cheating is a viable and respectable technique to succeed in Mexican. There are several ways to cheat, a few of which are mentioned here:
A player may attempt to flip one or more dice after looking at them but before (or while) lowering the cup over the top and passing the dice to the next player. However, a player being caught in the act of cheating MUST admit such and pass the dice to the next player. The cheater owes a drink, and the next player may roll "fresh." The key phrase is "in the act." Other players may judge this, but the honor system should prevail.
Another variation of cheating is to claim a roll that doesn't beat the previous roll. If the next player hasn't been paying attention, and believes the roller's claim, any previous roll to beat is null and void, and the cheater has no more obligation to the roll. This prevents players from socializing with more attractive persons while playing. Other players are free to share information about the current roll to beat, if asked by the distracted player—other players are also free to claim ignorance.
Cheating also includes any other methods by which the roller gains an unfair advantage over the next player. In all instances, the onus is upon the next player to ensure the roller is playing honestly. Again, other players are under no obligation to the roller or the player—they act independently. But this independence is absolute—they may (or may not) rule as a body for or against the roller or the victim.
In practice, this rule typically means that if a player is not paying attention, it's best for the player to believe the roll claimed, for obvious reasons.
Modern variants
Commercial versions
- 1974 Liars Dice, published by E.S. Lowe
- 1984 Liars Dice, Milton Bradley, designed by Richard Borg.
- 1993 Call My Bluff by FX Schmid, designer Richard Borg, won the 1993 Spiel des Jahres and Deutscher Spiele Preis awards.[4]
- 1994 Perudo published by University Games, designed by Cosmo Fry.
- 2001 Bluff, from Ravensburger (after acquiring FX Schmid), reissue of Call My Bluff, won the 2006 Årets Spel adult game of the year award.
- 2002 Liars Dice by Endless Games - 4 player variant.
- 2011 Diception by Four Clowns Game and Toy Co, - 4 Player game with Second Chance Cube to Change the Odds.
- 2011 Liar's Dice Live by FrontDev, - Multiplayer (up to six players) online Liar's Dice for Android.
See also
- Bullshit (card game) - a card game with a similar emphasis on bluffing and detecting bluffs.
- Liar's poker - a structurally similar game using the digits of the serial numbers on dollar bills
- Mia - a dice game with a similar emphasis on bluffing
- Diception - very similar to Liar's Dice but with a unique twist that changes the odds of the game.
In popular culture
In the film Pirates of the Caribbean: Dead Man's Chest, Liar's Dice plays an important role as a plot element, in that Will Turner plays a game of Liar's Dice with his father and Davy Jones; the end result is that Bootstrap Bill is forced to serve an eternity aboard the Flying Dutchman. In the Blu-ray release of the film, an interactive game is included where the viewer can play Liar's Dice against Pintel.
In the video game Pirates of the Caribbean: At World's End, Liar's Dice is known as "Pirate Dice" and is a playable mini game at some stages of the game.
In the video game Red Dead Redemption, Liar's Dice is a playable mini game in which the player can win or lose money.
In the video game Leisure Suit Larry: Love for Sail!, a variant called Strip Liar's Dice is a playable mini-game, which follows the same common ruleset as Liar's Dice, with the option to buy your lost dice back using articles of clothing.
References
- ^ Perudo.com; Perudo History Perudo
- ^ Instructables; How to Play Liar Dice
- ^ Hoyle's Rules of Games, Third Revised and Updated Edition. Albert H. Morehead and Georffrey Mott-Smith - Revised and Updated by Philip D. Morehead
- ^ Funagain Games; 1993 Spiel des Jahres